Conjunto Gerador

Surgiu uma pergunta muito interessante durante a última reunião (pergunta feita pelo Henrique). Ele perguntou-me sobre a definição de conjunto gerador feita pelo Elon e, na hora, não tinha me ocorrido o principal motivo para tal definição…

Fica muito difícil (não faz sentido) você definir soma infinita sem saber do que está tratando (aqui, eu quis dizer, sem uma topologia). Agora, vamos às definições.

Para ficar mais claro para todos (nclusive aos que não estão lendo o Elon agora), o Elon faz a seguinte definição:

SEJA $E$ um espaço vetorial. Se $X\subset E$ , o subespaço gerado $X$ é o espaço formado por

vetores do tipo $\sum_{i=1}^n k_i v_i$ (onde $v_i\in X$ , $k_i\in\mathbb{R}$ e $n\in\mathbb{N}$ (deve-se, primeiramente, provar que isso realmente é um subespaço).

Por que essa definição? A idéia de conjunto gerador de alguma coisa vem da idéia de menor (sub)estrutura que contém aquele conjunto.Ou seja, queremos saber qual o menor subespaço/subestrutura que contém aquele conjunto.

Assim acontece em vários assuntos: Em teoria dos grupos, o subgrupo gerado por um subconjunto de um grupo é, na verdade, o menor subgrupo que contém aquele conjunto…

Então, no caso que o Henrique expôs, note que $\mathbb{R}^{(\infty)}$ , de fato, é um subespaço, contém o conjunto dos vetores “canônicos” e é o “menor” espaço que contém aquele conjunto ( inclusive, $\mathbb{R}^{(\infty )}$ é subespaço (e subconjunto próprio) de $\mathbb{R}^{\infty}$ ).

Inclusive quem é bastante atento para esse fato e me falou sobre isso, no caso espacial da topologia, foi o André. Na topologia também tem uma coisa que se chama subbase (que gera a menor topologia que a contém).

Então, no caso do Elon, a definição foi feita assim para a definição ser equivalente à seguinte definição: O subespaço $S(X)$ gerado pelo conjunto $X$ é o menos subespaço topológico que contém $X$ .

Ele preferiu dar a definição como foi feita, pois ele deu uma definição construtiva de $S(X)$ . Não seria difícil, mas, se você usasse a definição acima, você deveria provar que construir o subespaço $S(X)$ equivale a pegar as combinações lineares finitas (na verdade, vc precisaria fazer isso para provar que $S(X)$ está bem definido)… Olha só: usando essa definição, vc teria que provar que está bem-definido (pois vc a princípio não sabe se realmente existirá um menor subespaço que contém aquele conjunto (vc deveria provar que existe e, então, chegaria à construção dele).

Bom, se o André quiser comentar alguma coisa sobre isso! 😀 😀 😀 😀 No caso da topologia (subbase), acho que tem uma prova “não-construtiva” de que a coisa está bem definida… não sei se há o mesmo para o caso do conjunto gerador (na álgebra linear).

Acho que não, né André?

Para os Pré-PIC’s de novo: página 19, questão 2.9 (acabei de encontrar aqui). Fazendo essa questão, vocês vão entender melhor do que eu estou falando… Dizer que $S(X)$ é a interseção de todos os subespaços vetoriais que contém o conjunto $X\subset E$ é o mesmo que dizer que: $S(X)$ é um subespaço e está contido em todos os subespaços que contém $X$ (ou seja, $S(X)$ é o menor subespaço que contém $X$ ).

This entry was posted on 0, 13 de agosto de 2009 at 9:31 pm and is filed under Álgebra Linear. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

6 Responses to Conjunto Gerador

andrecaldas disse:

agosto 15, 2009 às 3:48 am

Fernando,

Pra definir espaços vetoriais de dimensão infinita, ou subespaços de dimensão infinita gerados por um subconjunto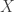 $X$ , não é necessário falar de somas infinitas. Para ser espaço vetorial, basta que as somas sejam finitas. 😉

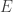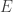Assim, mesmo para um espaço vetorial $E$ de dimensão infinita, se $X \subset E$ , então, fazendo $S(X) = \{ \sum_{k=1}^n k_i v_i : v_i \in X, k_i \in \mathbb{R}, n \in \mathbb{N} \}$ , é fácil ver que $S(X)$ é um subespaço vetorial de $E$ . Também é fácil ver que todo subespaço de 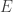$E$ que contém 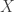$X$ , terá que conter todos os elementos de $S(X)$ . Assim, $S(X)$ é o menor subespaço que contém $X$ .

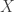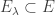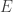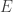É um pouquinho mais avançado, mas acho legal olhar para esses conceitos pensando em retículados completos. O que acontece, é que a interseção de um número qualquer de subespaços $E_{\lambda} \subset E$ é um subespaço de $E$ . Esta interseção é na verdade, o maior subespaço contido em todos os $E_{\lambda}$ . Assim, se considerarmos a família de todos os subespaços de $E$ ordenados pela inclusão (um subespaço é “maior” que outro se o contiver), teremos o conceito de “ínfimo”. Sempre que isso ocorrer, e a família também tiver um “máximo” ( 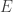$E$ é o maior subespaço de 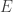$E$ !), então uma família de subespaços terá sempre um “supremo”, que será o “infimo” dentre os subespaços que os contém. (pergunta, por que é importante a observação: 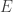$E$ é o maior subespaço de $E$ ?)

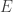Existem várias outras coisas que são ordenadas por inclusão e que a “interseção dessas coisas” também dá uma coisa do mesmo tipo. Por exemplo, a interseção de subespaços vetoriais é um subespaço vetorial. A interseção de subgrupos também é um subgrupo. A interseção de topologias de um conjunto também é uma topologia deste conjunto. A interseção de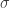 $\sigma$ -álgebras de um conjunto (teoria da medida) também é uma 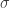$\sigma$ -álgebra deste mesmo conjunto. O mesmo vale para sub-anéis, ideais, corpos, grafos, etc.

Ficou meio complicado, né? Talvez eu formule melhor um outro horário… são 3:35AM! 😉
Ou melhor, se não entender, é só postar uma pergunta. =O)

Referências (em inglês):

Reticulado.
Reticulado Completo.

André Caldas.

Responder
- Lucatelli disse:
  
  agosto 15, 2009 às 7:01 pm
  
  Ah!
  Poxa! é mesmo! heehehehe… vacilei! Interseção de subespaços é um subespaço: nem sei o porquê de eu ter achado que não dava para provar que estava bem definido sem ser construtivamente… VALEU! hehehe
  
  Mas, quanto ao que eu coloquei em negrito agora, foi um comentário dirigido ao Henrique… Quando eu disse que não se pode pensar/”muito difícil pensar”/”não faz sentido pensar” em somas infinitas sem saber do que se está tratando, quis dizer que precisamos de uma topologia na parada para pensar em convergência.
  
  Olha só o que o Henrique tinha colocado:
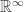  Seja $\left\{e_1,....,e_n,...\right\}$ um subconjunto do espaço vetorial $\mathbb{R}^\infty$ . Ele queria saber o porquê que o subconjunto não gerava $\mathbb{R}^\infty$ .
  Na verdade, ele queria substituir a definição do Elon pela definição usando somas infinitas: por isso que eu disse que não podemos usar somas infinitas. E, depois, ainda, justifiquei a definição do Elon com a idéia de conjunto gerador (que é a menor (sub)estrutura que contém aquele conjunto).
  
  Bom, muito obrigado pelo comentário,
  Abraço
  
  Responder
  - andrecaldas disse:
    
    agosto 15, 2009 às 8:05 pm
    
    Lembre-se de colocar um “espaço” depois da palavra “latex”. 😉
    
    Na verdade, ele queria substituir a definição do Elon pela definição usando somas infinitas: por isso que eu disse que não podemos usar somas infinitas. E, depois, ainda, justifiquei a definição do Elon com a idéia de conjunto gerador (que é a menor (sub)estrutura que contém aquele conjunto).
    
    Ah, sim. Entendi. É verdade, você está certo. E ele também… 🙂
    
    Eu lembro que eu também ficava incomodado com essa definição. Essa coisa do “menor que contém” é, na minha opinião, a melhor maneira de ver a coisa, realmente. Mas é bom lembrar que uma definição não é uma “verdade absoluta”. É só uma convenção. Um bom exercício para o Henrique é tentar formalizar uma definição para “subespaço gerado por um conjunto através de somas infinitas”. Lembre-se que existem vários tipos de infinito. O que é essa soma? (precisa da topologia como você bem colocou)
    
    Uma referência boa:
    
    Base de Hilbert.
    Base de Schauder.
    
    André Caldas.
  - Lucatelli disse:
    
    agosto 15, 2009 às 8:21 pm
    
    É! =)
    Muito bem colocado! heheheheheehe…
    
    Sobre o espaço entre o “latex” e o comando, eu já fiz vários testes: pode colocar sem espaço ou com espaço: de qualquer forma, compila. E, de qualquer forma, dá problema (fica um tempo para compilar).
    
    Muito bem colocado: “Lembre-se que existem vários tipos de infinito.”
    Mas, no caso do Henrique, ele não viu ainda… 😦
    Falei para ele dar uma olhada nisso (ou na internet, ou nas primeiras páginas do livro de análise).
    Por esses motivos e outros motivos, por eles ainda estarem no início e por eu mesmo não saber muita coisa de bases infinitas (só usei uma vez numa demonstração do PIC), preferi evitar o assunto. Por isso que, antes de eu falar que era preciso de uma topologia, tinha falado também que “tudo que fizermos é para espaços vetoriais de dimensão finita”.
    
    Mas gostei do exercício proposto para o Henrique! Ele realmente seria enriquecedor. Assim, ele mesmo perceberia o que está faltando…
    Para ele tentar fazê-lo falta a ele a noção de enumerabilidade (e não-enumerabilidade).
    
    Bom, massa! =) =)
    
    Acho que nossas discussões (e seus comentários) estão sendo bem construtivos! Espero que todo o público disso tudo (Henrique e Thiago) esteja aproveitando (ou vá aproveitar)! =)
    
    Abraço =)
    
    E obrigadão!! =)
  - Lucatelli disse:
    
    agosto 15, 2009 às 8:42 pm
    
    Poutz!
    QUE MASSA!
    Agora que vi o lance das somas infinitas (e bases enumaráveis) para espaços separáveis! 🙂
    Muito massa mesmo! =) hehehehehehe…
    =)
    =)
    =)
    =D
    =D
    =D
    =D
    
    VALEU! =)
  - Lucatelli disse:
    
    agosto 15, 2009 às 9:00 pm
    
    Agora, eu verifiquei! Parece que o espaço “ajuda” a compilar!
    Mas eu juro (para mim mesmo) que várias vezes fiz sem o espaço (quando, depois do “latex” há um comando (que inicia com a \)) e deu certo e, para mim, parecia que sem ou com espaço a “probabilidade” de demorar para compilar era a mesma!
    
    Mas, agora, estou vendo e me parece que é melhor colocar com espaço (ou talvez até seja obrigatório)