Variedades Flag de Posto Um São Esferas.

Da série “Entendendo a Tese do Lonardo”.

Teorema. Seja um grupos de Lie semissimples cuja álgebra de Lie tem posto real um, e tomemos um subgrupo parabólico (único a menos de conjugação). Então, a variedade flag é difeomorfa a , em que e é raiz simples.

Demonstração. Em geral, e , de modo que . Como o posto real de é um, temos . Resta provar que é uma esfera.

Para tanto, lembramos que é difeomorfo a , em que e são as decomposições de Iwasawa, e que é equivalente, como -espaço homogêneo, à órbita de um elemento regular por . A hipótese do posto real de ser um implica duas coisas: (i) para ser regular basta , e (ii) existe uma correspondência 1-1 entre elementos regulares de e subespaços abelianos maximais pela relação .

Escolhamos, então, um vetor tal que ( é forma de Cartan-Killing de , que é um produto interno quando restrita a ) e ponhamos . Como preserva , então . Reciprocamente, se e , então existe tal que , isto é, . Como todo elemento do grupo de Weyl admite representante em via , concluimos que para algum , ou seja, que . Isto prova que .

Aqui usamos a restrição para o . Tem como construir diretamente uma ação transitiva de numa esfera com isotropia ?

Conexidade da Compactificação de Um Ponto/Alexandroff

Todos vemos no curso de topologia que pode-se acrescentar um ponto a qualquer espaço topológico não compacto  para torná-lo compacto (a tal compactificação de um ponto, ou de Alexandroff, que denotaremos por ). Admitindo que é de Hausdorff e localmente compacto, tem-se que também possui essas propriedades. Além disso, uma vez que acaba sendo um subespaço denso de , tem-se adicionalmente que é conexo sempre que o for. (A recíproca dessa última afirmação não é verdadeira: se é a união de dois discos fechados que se tangenciam num ponto, menos esse ponto de tangência, então é desconexo apesar de ser conexo.)

A questão que eu gostaria de levantar é a seguinte: quais condições sobre garantem que é conexo por caminhos? Sem enrolar muito, o critério que encontrei é o seguinte:

Proposição: Se é um espaço topológico de Hausdorff não compacto, localmente compacto, conexo por caminhos e -compacto, então é conexo por caminhos.

Dem.: Seja uma família de subespaços compactos de tal que e . Dado , precisa-se mostrar que existe uma curva contínua tal que e , em que . Pode-se supor, sem perda de generalidade, que . Deste modo, seja uma sequência de pontos de tal que e para . Pela definição da topologia de tem-se . Como é conexo por caminhos, para cada existe uma curva satisfazendo e . Usando que é homeomorfo a por uma função crescente (e.g. , ), produz-se uma curva e uma sequência de pontos satisfazendo , e . A curva definida por para e satisfaz as condições desejadas. QED

Então, ser -compacto é suficiente, e desconfio que também é necessário, mas não consegui encontrar um exemplo que mostrasse isso. Se alguém achar, posta um comentário aí.

Product Type Dynamical Systems: variational principle

(English Below)

Este é um resumo do seminário que vou apresentar dia 26 de janeiro de 2012 no Imperial College London.

This is the abstract of a seminar I am about to present on 26 January of 2012 at the Imperial College London DynamIC Seminars. The slides will be upload to this page as soon as they are available.

Comments are very welcome, and can be made at the end of this page.

Abstract

Inspired by the Kolmogorov-Sinai entropy (KS-entropy) for a measure-preserving dynamical system, Adler, Konheim and McAndrew developed a purely topological concept of entropy (AKM-entropy) for topological dynamical systems over compact phase spaces. The AKM-entropy relates to the KS-entropy trough the so called Variational Principle: where is the AKM-entropy and is the KS-entropy for the dynamical system . The supremum is taken over all possible Borel measures.

Since then, many attempts to generalise this to non-compact spaces have been made. But not always the Variational Principle holds for this new concept. Bowen did it for metrizable systems. For a definition that uses some heavy machinery under the umbrella of topological pressure, Pesin and Pitskel’ have proved that the Variational Principle holds under some (hard to verify) hypothesis. In this Seminar, I will present a new concept of entropy which is surprisingly close to the AKM-entropy, and for which the Variational Princilpe still holds for a wide range of spaces. We have called those, Product Type Dynamical Systems.

Downloads

• Preprint: André Caldas & Mauro Patrão. Entropy and Its Variational Principle for Product Type Dynamical Systems.
• Slides: Presentation PDF.

Homotopia de flags I

Não sei se existe na literatura uma descrição dos grupos de homotopia das variedades flag.
Alguns casos eu consigo ver, usando resultados conhecidos e poucos recursos, como a sequência exata de fibração.
Por exemplo, um flag maximal associado a um grupo complexo é o quociente de um grupo compacto por um toro . Dos grupos de homotopia do toro só tem o grupo fundamental , os outros são triviais (isso porque uma aplicação de recobrimento induz isomorfismo nos grupos de homotopia de 2 em diante e é contrátil). Então, na sequência exata

o primeiro termo desaparece a partir de n = 2, o que implica que a partir de n = 3 os grupos de homotopia dos flags são isomorfos aos grupos de homotopia do grupo. (Os casos n = 1 e n = 2 podem ser tratados separadamente.) Por outro lado, para os grupos compactos clássicos (SU(k), SO(k) e Sp(k)) os seus grupos de homotopia \pi_n são conhecidos, desde que n seja bem menor que k (tem gente que gosta de chamar isso de homotopia estável, porque eles são na verdade os grupos de homotopia dos grupos infinitos). Isso é o resultado do teorema de periodicidade de Bott (que pode ser encontrado, por exemplo, no livro Husemoller, Fibre Bundles).
Ainda com os flag maximais, dá para tratar também dos grupos que são formas reais normais, isto é, em que o posto real coincide com o posto (os clássicos são Sl(n,R), SO(p,p+1), Sp(n,R) e SO(p,p)).
Nesses casos o flag maximal é o quociente K/M de um grupo compacto K por um grupo finito M. Portanto a projeção é um recobrimento, que induz isomorfismo nos grupos de homotopia a partir de n = 2 (vou comentar depois sobre o grupo fundamental dos flags em geral).
Para os outros flags maximais o grupo M pode não ser toro e certamente não é discreto.
Outro caso que admite um tratamento semelhante é o dos flags de subespaços de de dimensões 1,2,…,k com k<n, isto é, , real ou complexo. O que acontece aqui é a variedade de Stiefel (seus elementos são os conjuntos de k vetores l.i) fibra sobre , sendo que a fibra é um toro no caso complexo e é discreta no caso real. Além do mais, a homotopia estável de (isto é, com m pequeno em relação a n-k) é zero (isso também pode ser encontrado no livro do Husemoller. Aliás é essa propriedade de que faz com que os fibrados de Stiefel sejam universais.)  Portanto, tem homotopia (estável) trivial. Talvez seja possível obter informações sobre os grupos de homotopia de outros flags, via a sequência exata de fibração. Em todo caso tem que ser alguma coisa tipo homotopia estável. O cálculo do grupos de homotopia, com toda generalidade, é muito dificil, mesmo para a esfera.

Conjunto de Cantor

Neste post, vou fazer uma exposição breve sobre o conjunto de Cantor (sob uma perspectiva que eu adotei). Este post usará as considerações do post. Aqui, vou definir o espaço/conjunto de Cantor como sendo o prodtuo de espaços topológicos discretos .

Tem-se, pelo teorema de Tychonoff, que 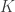é compacto. Além disso, pelas considerações do post, segue que 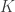é homeomorfo a (qualquer que seja o ) e, também, é homemorfo a .

O conjunto de Cantor é originalmente construído na reta. Aqui, vou definir conjunto de Cantor na reta como sendo qualquer imersão topológica do espaço 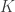na reta. Ou seja, se é um homeomorfismo sobre sua imagem, 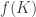será chamado de um conjunto de Cantor.

Uma observação óbvia é que, por 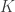ser compacto, tem-se que toda injeção contínua é uma imersão topológica (pois seria uma bijeção contínua de um compacto num Hausdorff (portanto um homeomorfismo)).

Seguindo essa definição de conjunto de Cantor na reta, um exemplo de conjunto de Cantor na reta é construído no post sobre curvas de Peano.

Teorema 1: Seja o espaço/conjunto de Cantor. Tem-se que 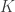é compacto, totalmente desconexo, não possui pontos isolados e é não-enumerável.

Demonstração: Pelo teorema de Tychonoff, como é evidentemente compacto, segue que o produto é compacto.

Além disso, é fácil verificar que 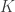é não-enumerável: com, por exemplo, argumento da diagonal de Cantor. Mas, para fazer uma verificação rápida desse fato, é fácil construir uma bijeção de 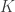com o conjunto das partes de (de fato, a cada subconjunto de 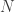, associa-se a sua “função característica”). Como o conjunto das partes de não é enumerável, segue que 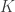não é enumerável.

Pela própria definição da topologia produto, não há como 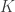possui pontos isolados. De fato, todo aberto de 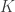deve ter uma projeção em cuja imagem é o espaço todo (pela definição da topologia produto). Logo, dados 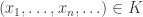e uma vizinhança aberta desse ponto, segue que existe tal que . Mas isso quer implica que , onde . Isso, então, provou que todos pontos de 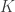são não isolados.

Para encerrar a demonstração, prova-se que 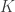é totalmente desconexo (ou seja, as componentes conexas de 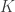são unitárias). Com efeito, dada uma componente conexa , segue que as imagens de pelas projeções devem ser conexas. Mas as únicas componentes conexas de são os pontos. Então, para todo 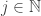, é unitário. E, portanto, é unitário. E isso, então, completa a prova de que 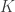é totalmente desconexo.

CQD

Seguem as propriedades conhecidas do conjunto de Cantor na Reta. Abaixo, estão enunciadas e provadas.

Corolário 1.1: Seja um conjunto de Cantor. Segue que é compacto, tem interior vazio, não contém pontos isolados e é não-enumerável.

Demonstração: Com efeito, pela definição, tem-se que é homemorfo a . Logo, pelo teorema 1, tem-se que é compacto (portanto limitado e fechado), é não enumerável e não contém pontos isolados.

Além disso, tem-se que é totalmente desconexo. Em particular, todos subconjuntos conexos de são unitários. Disse segue que não contém intervalos e, portanto, possui interior vazio.

CQD

Aqui, o post ficaria completo. Foram definidos os conjuntos de Cantor. Além disso, este último corolário mostrou que os conjuntos de Cantor na reta possuem as propriedades interessantes esperadas do conjunto de Cantor. Mas, antes de encerrar o post, será provado que o conjunto de Cantor usual (como, por exemplo, é definido nos livros livros de análise) é um conjunto de Cantor segundo a definição deste post.

Não vou colocar, aqui, a definição usual. Muito menos discutí-la em detalhes. Acho que tem lugares onde isso pode ser encontrado (como wikipedia ). Denotemos por 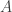o esse conjunto de Cantor usual. Uma das observações interessantes de se fazer é que o conjunto 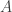é construído de tal forma que seus números na base 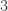sejam escritos com os algarismos 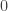e 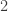somente. Na primeira etapa, tira-se o conjunto dos números, onde na base 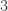tem . Na etapa 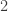, tiram-se os números onde na base .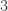

No final da construção, o conjunto 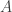fica sendo o conjunto dos pontos tais que podem ser escritos na base 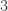apenas com os algarismos 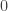e .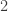

Define-se no conjunto de Cantor 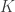a métrica . E, então, define-se a aplicação , onde .  Pelas considerações acima, segue que isso está bem definido e é uma sobrejeção. Além disso, é contínua e é fácil verificar que é injetiva. Portanto é uma bijeção contínua.

Como 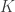é compacto e 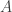é Hausdorff, segue que é um homeomorfismo. Portanto, de fato, 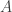é um conjunto de Cantor.

Curvas de Peano

Neste post todo, o intervalo será denotado por . Seja um espaço métrico. Uma curva de Peano em é uma aplicação contínua sobrejetiva.

Essas curvas de Peano tem relação (evidente) com o “cálculo” de grupos fundamentais. Em particular, a existência dessas curvas de Peano, por exemplo, está relacionada com a prova de que é simplesmente conexo para . Isso será explicado em outro post.

Aqui, vou construir de forma direta uma curva de Peano em , qualquer (por exemplo, é o quadrado fechado). Para isso, vou utilizar algumas considerações do post anterior.

Segue, abaixo, mais um lema sobre extensão contínua que será importante para a construção das curvas de Peano.

Lema 1: Seja um subconjunto fechado. Se é um conjunto convexo, segue que qualquer aplicação contínua possui extensão contínua .

Demonstração: Com efeito, pela estrutura (topológica) da reta, tem-se um resultado conhecido de que todo aberto pode ser escrito como uma reunião enumerável de intervalos abertos disjuntos. Logo é escrito como uma reunião enumerável de intervalos abertos . Logo define-se , se . E, para , tem-se que para algum e, nesse caso, define-se . Verificar que é, de fato, contínua é fácil. Além disso, pode-se notar que está definida nesses intervalos abertos como sendo o segmento de reta que liga os valores de nos extremos.

CQD

Antes de construir a curva de Peano, seguem algumas definições e um lema importante para a construção.  Seja o espaço topológico (metrizável) munido da topologia discreta.

Segue que é um produto de espaços e, munido da topologia produto, é metrizável. Pelo teorema de Tychonoff, segue que é compacto. E, pelas considerações do post anterior, tem-se que é homeomorfo a (para qualquer ) .

Lema 2: Seja o produto dos espaços topológicos discretos. Existe uma aplicação contínua sobrejetiva .

Demonstração: Define-se uma métrica em . Dados , define-se . E, então, a aplicação tal que , denotando-se ,  é evidentemente contínua e sobrejetiva. Logo, dado , é uma aplicação contínua sobrejetiva. Seja, então um homeomorfismo. Segue, então, que é uma aplicação contínua sobrejetiva.

CQD

Teorema de Peano: Para qualquer , existe uma aplicação contínua sobrejetiva.

Demonstração: Mune-se da seguinte métrica coerente com a topologia produto .

Define-se, então, a aplicação contínua tal que . É fácil verficar que é injetiva. Define-se . Tem-se, então, que é compacto (e, em particular, fechado em ). Além disso, tem-se que , onde , é uma bijeção contínua definida num compacto que toma valores num espaço Hausdorff. Portanto  é um homeomorfismo e, então, e são homeomorfos.

Dado , toma-se a aplicação contínua sobrejetiva , cuja existência é garantida pelo lema 2. Portanto é uma aplicação contínua sobrejetiva. Pelo lema 1, segue que existe uma extensão contínua (sobrejetiva) de .

CQD

Homeomorfismo do Produto

O que vou expor aqui está intimamente ligado com o post sobre Conjunto de Cantor e com o post sobre Curvas de Peano (que serão feitos nos próximos dias). O post será breve: apenas para expor um resultado simples. Antes de falar de produto de espaços topológicos, é importante relembrar a definição de topologia produto. E, para isso, há um post muito bem escrito pelo André.

Aqui, vou fazer apenas uma discussão breve sobre uma propriedade da topologia produto. A pergunta é: “Quando um espaço topológico é homeomorfo ao espaço ?” (Existem espaços que satisfazem isso (por exemplo, um ponto). E, como pode ser visto no post, o conjunto de Cantor satisfaz essa propriedade).

Seja um espaço topológico. Se é homeomorfo a , é fácil ver, fazendo uma indução óbvia, que é homeomorfo a (para qualquer ). Isso seria, portanto, uma condição necessária.

Neste post, não me preocuparei em procurar uma condição “necessária e sufieciente”, vou apenas destacar uma condição suficiente. Uma condição suficiente para que seja homeomorfo a é que seja homeomorfo a um produto de um espaço topológico qualquer. Isso será enunciado e provado abaixo.

Lema 1: Sejam espaços topológicos. Se é homeomorfo a , segue que é homeomorfo a e a (para qualquer ).

Demonstração: Com efeito, basta provar que é homeomorfo a e a .  Define-se a aplicação

, onde .

Ou seja, dada uma seqüência , tomam-se as as subseqüências dos termos de índice ímpar e a subseqüência dos termos de índice par . E, então, define-se . É fácil de verificar que essa aplicação é bijetiva. E, usando as projeções, é fácil verificar que é um homeomorfismo.

E, seja uma partição de em conjuntos infinitos .

De fato, bastava tomar, para , o conjunto , onde é o -ésimo primo. E, então, bastava fazer .

Define-se , onde . E, de forma análoga, é fácil ver que é uma bijeção e, também, é fácil verificar que é um homeomorfismo.

CQD

E, para completar esse post, vou expor uma conseqüência óbvia.

Conseqüência: Seja um espaço topológico. Para ser homeomorfo a é necessário e suficiente que seja homeomorfo a algum produto de espaços topológicos .

Grupo Fundamental de Grupos Topológicos

Uma das características interessantes do functor grupo fundamental é que nem todo espaço topológico possui grupo fundamental abeliano. Por exemplo, todas superfícies compactas de gênero maior ou igual a possuem grupo fundamental não abeliano.

Vou mostrar, neste post, que todos grupos fundamentais de um grupo topológico são isomorfos. Além disso, vou provar qu eles são abelianos. Isso tem algumas implicações interessantes. Por exemplo, se um espaço topológico possui grupos fundamentais não-abelianos, segue que não admite uma estrutura de grupo que o torne um grupo topológico.

Teorema 1: Seja um grupo topológico. Todos grupos fundamentais de são isomorfos entre si.

Demonstração 1: Com efeito, se os pontos base de dois grupos fundamentais estiverem na mesma componente conexa por caminhos, segue que eles são isomorfos. Caso contrário, é fácil ver que quando é a componente conexa por caminhos de (isso é bem tranqüilo de provar, mas talvez eu comente (ou demonstre) em algum post).  Como todas componentes conexas por caminhos num grupo topológico são homeomorfas entre si, segue que elas têm o mesmo grupo fundamental.

CQD

Sejam um grupo topológico e seu elemento neutro. Toma-se a componente conexa por caminhos do elemento neutro (que é um subgrupo topológico). Será provado que possui grupo fundamental abeliano.

Define-se no grupo fundamental uma outra operação. Dados (onde são caminhos com base ), define-se , onde , com (aqui, denota a operação no grupo ). Resta provar que a operação está bem definida.

Primeiramente, prova-se que é, de fato, um caminho com base em . Com efeito, tem-se que , ou seja, é composição de aplicações contínuas e, portanto, é contínua. Além disso, tem-se que . Portanto, de fato, . Resta provar que a definição não apresenta ambigüidade. Dados no grupo fundamental , segue que existem homotopias e relativas ao ponto . Logo é fácil de verificar que tal que é uma homotopia entre e relativa ao ponto . Isso provou que . E, portanto, isso completou a prova de que a operação está bem definida.

Teorema 2: Seja um grupo topológico. Todos grupos fundamentais de são abelianos. Além disso, o produto acima definido coincide com a operação usual no grupo fundamental.

Demonstração: Com efeito, pelo provado no teorema 1, basta provar que o grupo fundamental da componente conexa por caminhos do elemento neutro é abeliano. Sejam essa componente conexa por caminhos e o caminho constante. Dados , é fácil verificar que

Isso provou as duas afirmações do teorema.

CQD

Com esse teorema, podemos, por exemplo, concluir que, para , um – toro não admite estrura de grupo que o torne um grupo topológico. Além disso, é com esse teorema que vou provar, futuramente, que se , o n-ésimo grupo de homotopia de um espaço é necessariamente abeliano. Ou seja, dentre os grupos de homotopia, só o grupo fundamental pode não ser abeliano!!!

Outro lema sobre extensão

Sejam um espaço topológico e . Diz-se que é um retrato de se existe uma aplicação contínua tal que para todo . Isso, em termos de extensão contínua, pode ser colocado da seguinte forma é um retrato de se a aplicação possui extensão contínua . A extensão contínua é chamada de retração.

Aqui, vou apresentar um lema sobre extensão que, na verdade, é uma caracterização de retratos de espaços.

Lema 1: Seja um espaço topológico. Um subespaço é retrato de se, e somente se, toda aplicação contínua possuir uma extensão contínua .

Demonstração: Com efeito, se toda aplicação possui extensão contínua, segue, em particular, que possui extensão contínua . Logo é retrato.

Reciprocamente, se é um retrato, toma-se a retração . Dada contínua, segue que é uma extensão contínua de .

CQD

Sejam um espaço topológico e . Uma retração é chamada de retração por deformação se ela for, também, uma equivalência homotópica com inverso homotópico sendo a inclusão .

Usando o lema sobre extensão, segue um resultado interessante: todo retrato de um espaço contrátil é contrátil. Afinal, se é um espaço contrátil e é retrato do espaço , segue que possui extensão contínua. E, pelo lema sobre extensão , isso implica que é homotópica a uma aplicação constante. Portanto é contrátil.

Outra forma de provar isso, é vendo que, se é um espaço contrátil, toda retração com domínio em é uma retração por deformação. Afinal, se é uma retração, tem-se que a inclusão   é homotópica a alguma aplicação constante. Logo e é homotópico a uma aplicação constante. Como é contrátil, segue que , por ser homotópico a uma aplicação constante, é homotópico à aplicação identidade. Isso provou que, de fato, é uma equivalência homotópica e, portanto, contrátil.

Espaços Contráteis

Este post apresenta alguns comentários soltos sobre Espaços Contráteis e algumas relações desses comentários com o que já foi feito em outros posts. Um espaço contrátil é um espaço topológico que tem o mesmo tipo de homotopia de um ponto.  Uma caracterização de espaço contrátil é: “Um espaço topológico é contrátil se, e somente se, a aplicação identidade é homotópica a alguma aplicação constante”. Neste post, vou apresentar uma pequena variação dessa caracterização. Ambas caracterizações são usadas no post sobre teorema do ponto fixo de Brouwer, no entanto, a segunda não é assumida (é provada no contexto da demonstração do lema 1).

Seja um espaço topológico. Uma involução (contínua) em é uma aplicação contínua bijetiva cuja inversa é a própria . Ou seja, . Evidente que, nesse caso, toda involução é um homeomorfismo. Um exemplo trivial de involução é a aplicação identidade.

Proposição 1: Sejam um espaço topológico qualquer e uma involução qualquer. é contrátil se, e somente se, é homotópica a uma aplicação constante.

Demonstração: Com efeito, se é contrátil, segue que o conjunto das classes de homotopia

é unitário. E, portanto, todas aplicações são homotópicas entre si. Em particular, é homotópica a alguma aplicação constante. Reciprocamente, se é homotópico a uma aplicação constante, segue que é homotópico a uma aplicação constante. Seja , essa aplicação constante homotópica a . Segue, então, que e

são equivalências homotópicas, afinal . E é homotópico à aplicação identidade em . Logo, de fato, é contrátil.

CQD

Note que, na demonstração e no enunciado da proposição, está incluida a primeira caraterização enunciada nesse post. Além disso, assumindo que não é contrátil (coisa que ainda vou demonstrar), essa proposição implica que a aplicação antípoda (que é uma involução) não é homotópica a nenhuma aplicação constante. E, então, disso e do resultado apresentado no post, segue diretamente o seguinte o lema 1 do post sobre ponto fixo de Brouwer enunciado abaixo como “lema de Brouwer” (por ser intimamente ligado com o teorema do ponto fixo de Brouwer):

Lema de Brouwer: Se é uma aplicação contínua homotópica a uma aplicação constante, então possui pontos fixos.

Demonstração: Bom, segue dos comentários que, por ser homotópico a uma aplicação constante, não é homotópico à aplicação antípoda . E, portanto, possui pontos fixos.

CQD

Mas, como eu comentei anteriormente, esse lema poderia ser ainda mais forte. Como não é contrátil, tem-se, pelo provado, que qualquer involução (em particular, a identidade) em não é homotópica a uma constante. E, portanto, tem-se o seguinte lema.

Lema 3: Se é homotópico a uma aplicação constante, então existem tais que e .

Demonstração: A existência do ponto fixo está provada no lema de Brouwer. Como é homotópico a uma aplicação constante, segue que não é homotópico à aplicação identidade. Logo existe tal que .

CQD

Voltando aos comentários sobre espaços contráteis, seguem alguns resultados elementares (e bem importantes) sobre classes de homotopia e espaços contráteis.

Proposição 4: Sejam um espaço contrátil e um espaço topológico qualquer. Segue que toda aplicação contínua é homotópica a alguma aplicação constante. E, por outro lado, toda aplicação contínua é homotópica a qualquer aplicação constante.

Demonstração: Seja uma aplicação constante homotópica à aplicação identidade em . Dada contínua, segue que é homotópico à . Como é constante, ficou provado que é homotópico a uma aplicação constante.

Por outro lado, tem-se que a família das classes de homotopia tem a mesma cardinalidade que . Como a última família tem carinalidade evidentemente igual a , segue que tem cardinalidade . E, portanto, todas as aplicações são homotópicas entre si. Em particular, qualquer aplicação contínua é homotópica a qualquer aplicação constante.

CQD

Desse simples resultado, segue uma generalização do lema sobre extensão.

Lema 5: Sejam um espaço topológico contrátil, e uma aplicação contínua. Se existe uma extensão contínua de , então é homotópico a uma aplicação constante.

Demonstração: Com efeito, tem-se, pela proposição 4, que a inclusão é homotópica a uma aplicação constante . Logo é homotópica à (que é constante).

CQD

Como todo convexo é contrátil, isso, da fato, generaliza o lema sobre extensão.