Aqui, estou precisando de uma coisinha para completar um raciocínio… Olha só:
“Seja uma função. E seja
o conjunto de pontos de continuidade dessa função. Segue que
pode ser escrito como uma interseção enumerável de abertos.”
Isso é verdade? Se for, eu queria a demonstração. Se não for, preciso de um contra-exemplo.
Abraço
E
Valeu
Vou tentar…
Considere as seguintes famílias de coberturas abertas de :
:
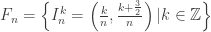 .
.
Então, basta mostrar que
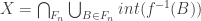 .
. é o interior do conjunto.
é o interior do conjunto.
Onde
Para mostrar que está contido no conjunto da direita, basta notar que
está contido no conjunto da direita, basta notar que 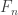 é uma cobertura e que portanto, para todo
é uma cobertura e que portanto, para todo  , existe
, existe  tal que
tal que 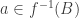 . Em particular, se
. Em particular, se 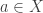 , então
, então 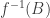 é vizinhança de
é vizinhança de  . Ou seja,
. Ou seja, 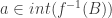 .
.
Para a outra inclusão, tomando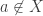 , basta seguir o seguinte roteiro:
, basta seguir o seguinte roteiro:
Escolha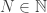 , tal que para todo
, tal que para todo 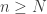 , existe um único
, existe um único  , tal que
, tal que 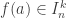 .
. não é ponto de continuidade, escolha
não é ponto de continuidade, escolha 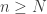 , e
, e  , tal que
, tal que 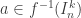 , mas
, mas 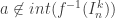 .
.
Como
Pelo primeiro item, se , então
, então 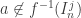 . Pelo segundo item,
. Pelo segundo item, 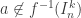 . Ou seja, para o
. Ou seja, para o  escolhido,
escolhido, 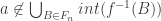 .
.
Acho que dá pra fazer um raciocínio parecido para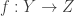 quando
quando  é compacto com base enumerável
é compacto com base enumerável  . Tomando, ao invés de
. Tomando, ao invés de 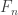 , as famílias de coberturas finitas formadas por elementos da base
, as famílias de coberturas finitas formadas por elementos da base  .
.
Um abraço,
André Caldas.
Tô achando que não é tão fácil escolher ! 😦
! 😦
Poxa!
EU achava que era mais direto!! =( =(
Mas eu acho que já saquei como fazer, no entanto, o objetivo disso era provar uma coisa massa (que já encontrei outra demonstração sem usar isso (e usando isso)).
Olha só para que eu queria isso:
“PROVAR QUE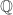 não pode ser o conjunto dos pontos onde uma função
não pode ser o conjunto dos pontos onde uma função 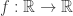 é contínua.”
é contínua.”
Definição: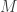 é chamado topologicamente completo, quando existe um espaço métrico completo
é chamado topologicamente completo, quando existe um espaço métrico completo 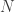 homeomorfo a
homeomorfo a 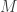 .
.
Um espaço topológico
Definição:
Um subconjunto de um espaço métrico diz-se magro, se é uma reunião enumerável de conjuntos cujos fechos tem interior vazio.
Então temos os seguintes teoremas:
LEMA: Seja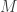 um espaço métrico completo. Se
um espaço métrico completo. Se 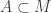 é aberto, segue que
é aberto, segue que 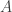 é topologicamente completo.
é topologicamente completo.
LEMA 2: Se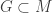 é uma interseção enumerável de abertos de um espaço métrico completo
é uma interseção enumerável de abertos de um espaço métrico completo 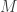 , então
, então 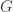 é topologicamente completo.
é topologicamente completo.
TEOREMA DE BAIRE: Seja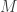 topologicamente completo. Todo subconjunto magro em
topologicamente completo. Todo subconjunto magro em 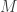 tem interior vazio.
tem interior vazio.
COROLÁRIO: Seja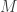 um espaço métrico topologicamente completo. Se
um espaço métrico topologicamente completo. Se 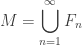 , onde cada
, onde cada  é fechado em
é fechado em 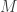 , então
, então 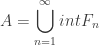 é um aberto denso em
é um aberto denso em 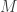 .
.
Bom, então, chega-se ao resultado particular: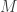 é enumerável e topologicamente completo, segue que o conjunto dos pontos isolados
é enumerável e topologicamente completo, segue que o conjunto dos pontos isolados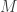 .
.
Se
é denso em
Isso prova que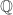 não é topologicamente completo, afinal o conjunto dos pontos isolados é vazio. =)
não é topologicamente completo, afinal o conjunto dos pontos isolados é vazio. =)
Em particular, ele não é uma interseção enumerável de abertos: daí eu queria uma coisa direta para mostrar que isso implica oq eu eu quero provar.
1. Achei sua definição de topologicamente completo meio complicada. Que tal: “um espaço topológico é topologicamente completo quando é completo em alguma métrica compatível com sua topologia.”
é topologicamente completo quando é completo em alguma métrica compatível com sua topologia.”
2. O primeiro LEMA é fácil de demonstrar? Qual é a cara dessa métrica?
3. Como assim “conjunto dos pontos isolados”?
Eu achei a minha “quase demonstração muito mais bonita”! =P
Falei bobagem, já que você tá demonstrando uma outra coisa… 😉
Um abraço,
André Caldas.
Isso!
Eu estava falando o porquê precisava disso… e o porquê queria que fosse direto!! =) =)
Falou
Olha só!!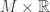 ) lá.
) lá.
O Primeiro lema é facinho de demonstrar… Você demontra que o conjunto aberto é homemorfo a um gráfico fechado (fechado em
se você quiser, eu coloco aqui depois!! 🙂
“Subconjunto dos pontos isolados”
Seja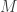 um espaço métrico enumerável topologicamente completo.
um espaço métrico enumerável topologicamente completo.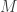 :
:
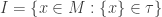 , onde
, onde  é a topologia de
é a topologia de 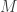 .
.
Segue que o seguinte conjunto é denso em
EU gostei da sua “quase-demonstração”. E vou ler a “segunda tentativa”! =) =) =) =) =) 🙂 🙂
Também achei bonita!!
Abraço
“Achei sua definição de topologicamente completo meio complicada. Que tal: “um espaço topológico M é topologicamente completo quando é completo em alguma métrica compatível com sua topologia.””
É a mesma coisa!! Mas eu tirei o métrico e coloquei topológico para você (eu poderia colocar metrizável).
Falou
P.s.: O fato é que, normalmente, quando vai provar que algum espaço é topologicamente completo, você prova que ele é homeomorfo a um espaço métrico completo e, depois, induz a métrica (daí nem precisa induzir a métrica na demonstração: é imediato).
Segunda tentativa…
Considere as seguintes famílias de coberturas abertas de :
:
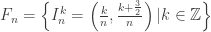 ,
,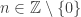 e
e 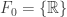 .
.
onde
Então, basta mostrar que
 .
. é o interior do conjunto.
é o interior do conjunto.
Onde
Para mostrar que está contido no conjunto da direita, basta notar que
está contido no conjunto da direita, basta notar que 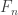 é uma cobertura e que portanto, para todo
é uma cobertura e que portanto, para todo  , existe
, existe  tal que
tal que 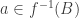 . Em particular, se
. Em particular, se 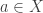 , então
, então 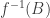 é vizinhança de
é vizinhança de  . Ou seja,
. Ou seja, 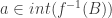 .
.
Para a outra inclusão, tomando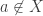 , note que:
, note que:
1. Se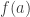 estiver contido em dois conjuntos da família
estiver contido em dois conjuntos da família 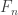 , então estará contido em um único conjunto de
, então estará contido em um único conjunto de 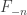 .
.
2. Como não é ponto de continuidade, existe uma bola de raio
não é ponto de continuidade, existe uma bola de raio  em torno de
em torno de 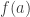 ,
, 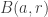 , tal que
, tal que  não é vizinhança de
não é vizinhança de  .
.
Escolhendo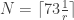 (dava pra pegar um pouquinho menor ;-)), teremos que existem
(dava pra pegar um pouquinho menor ;-)), teremos que existem 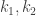 , tais que
, tais que 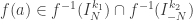 , mas nem
, mas nem 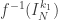 , nem
, nem 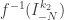 são vizinhanças de
são vizinhanças de  . Basta notar que ambos estão contidos em
. Basta notar que ambos estão contidos em 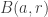 do item 2.
do item 2.
Assuma, pelo item 1, que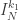 é o único elemento de
é o único elemento de 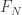 que contém
que contém 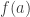 . Caso contrário, tomamos
. Caso contrário, tomamos 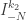 . Temos que
. Temos que  para nenhum
para nenhum 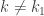 . E, pelo item 2, temos que
. E, pelo item 2, temos que 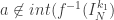 . Portanto,
. Portanto, 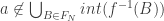 .
.
André Caldas.